Modeling Bach With Finite State Machines and Markov Chains

Modeling

I spend a lot of time working with models. Specifically, computational or mathematical models that approximate natural distributions. Language Models, for example, seek to approximate natural language. Generative image models approximate the space of all real-world images. The recent generative AI boom has given rise to many huge models with impressive capabilities. While scaling models has led to impressive performance, models don't always need to be enormous.

Big generative AI models require too much memory to be run on a normal computer. When you use ChatGPT, it is being run remotely on specialized hardware. There's an energy component as well: It is estimated that ChatGPT uses 17,000 times as much electricity as the average U.S. household every day. While these models have amazing capabilities, they're simply not needed for every task. Some things can be modeled quite effectively using very simple techniques such as linear regression. These lightweight techniques have several advantages over deep learning models including easy interpretability, simplicity, and low energy and memory cost.

Last year, I trained a language model to generate piano music, which turned out pretty well. However, it did suffer from several of the issues mentioned above. It was memory intensive and required a bunch of technical know-how to use. Since then, I've wanted to see how simple a model can be that still creates decent music.

I just finished with a class called computational creativity, where I built an interactive user interface for writing and displaying short pieces of music. With an intuitive way to manipulate music, I felt ready to build a simple model that creates music in the style of J.S. Bach.

Bach

Johan Sebastian Bach was born in Germany in 1685. He was an incredibly prolific composer, writing over 1000 pieces in his 65 years. His influence on modern music is immense, and he is widely considered one of the most important composers of all time.

Bach was a devout Lutheran, and among his works are nearly 400 chorales. (4-part hymns sung by Lutheran congregations) These works are in the public domain and all sound kind of similar.

These chorales have a long history of use in the machine learning context. Early neural music generation systems were trained on Bach's works, partly because of their closed domain (only 400 songs) and similarity to each other. A system trained on Bach's chorales only has to learn one very specific type of music. The first AI-powered Google Doodle was trained on the Bach chorales. Their prevalence in machine learning means a dataset of all the Bach chorales is available in a convenient, computer-readable format.

The JS Chorales dataset consists of 382 chorales. The data is optimized to be read by a computer, so it may not be very intuitive to you or I. In the dataset each beat is represented as a list of MIDI note numbers that correspond to pitches. For example, the first chord in this song is [65, 60, 57, 53] which corresponds to playing the notes [F, C, F, A] (an F major chord) on an instrument. The dataset is available in three resolutions. Chords can be sampled every quarter, eighth, or sixteenth note.

Finite State Machines

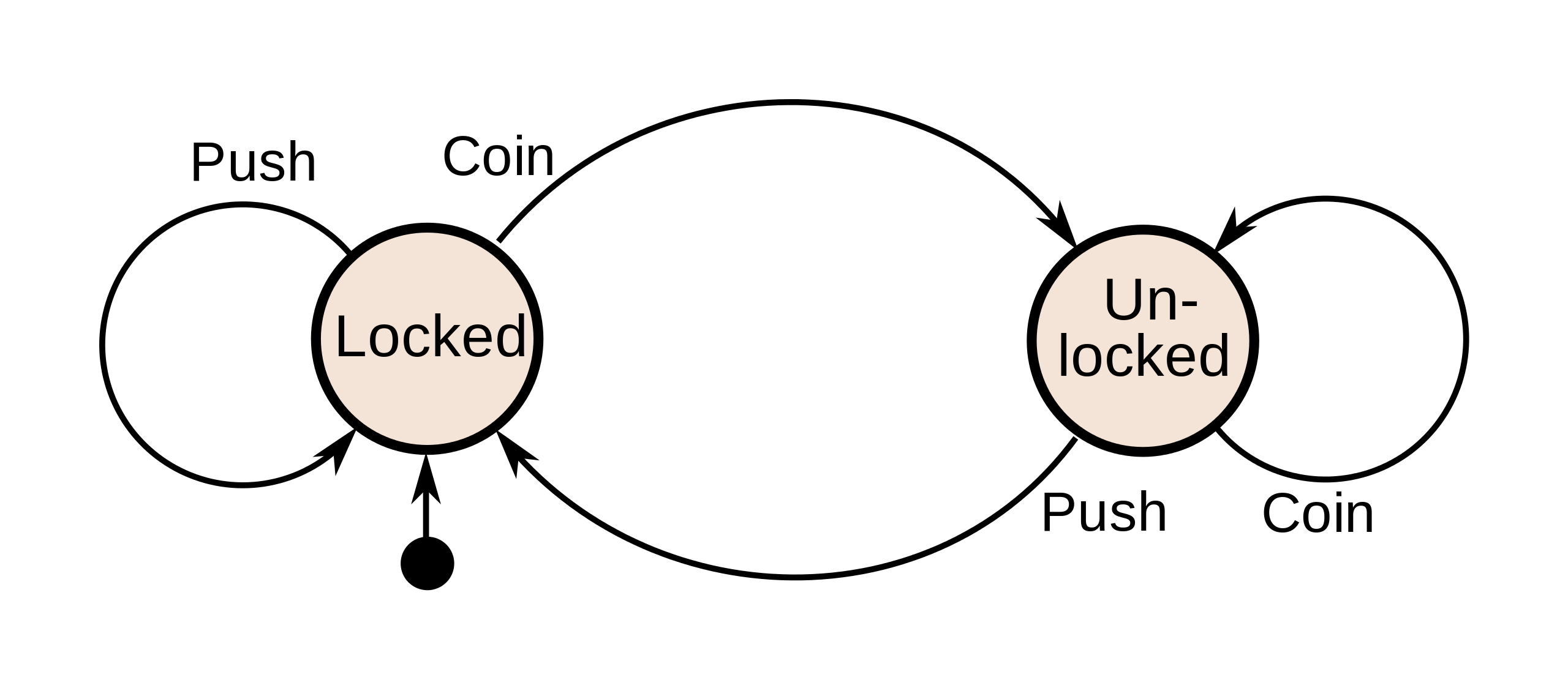
In thinking about Bach's chorales, I realized they could probably be modeled using something called a finite state machine. A finite state machine or finite state automaton is a mathematical model of computation. They are used to model a system that takes one of several states, with the possibility of transitioning between the states. This may be an unfamiliar concept, so here's an example adapted from Wikipedia:

Imagine a coin-operated turnstile, the type you might see in a train station. You go up to the turnstile and push on it, but you can't get through. The state of the turnstile is locked. Pushing on the turnstile does not change the state. Now you put in a coin. The state of the turnstile is now unlocked. You push through the turnstile and it locks behind you. The turnstile's state is back to locked.

The diagram below is a state diagram. It represents the turnstile example. It has a circle for each state, and an arrow for each possible state transition.

So why model Bach's chorales with a finite state machine?

Across all of Bach's chorales, there are only about 6,000 distinct chords. The dataset is already in a convenient format, with each chord representing a state. Going through the songs, we can see the state (chord) change as each song progresses.

We could imagine creating a state machine with 6,000 nodes, one for each chord. Then we could go through all of the chorales and every time a chord in the song changes to a different chord, we would draw an arrow between those two chords in our state machine. Pretty soon, we would have a computational model that captures all of Bach's chorales.

Markov Chains

If we had this theoretical state machine, how could we use it? We'd need to turn it into something called a Markov chain, named for Russian statistician Andrey Markov. To make the state machine into a Markov chain we'd go over every chord in all of Bach's chorales. For each state we'd count up all of the times that chord transitions to another chord, and then normalize over the total transitions. This would give us a probability for each state change. Then, we would have a stochastic (probabilistic) model of all of Bach's chorales.

To really be a Markov chain, we have to apply something called the Markov assumption. This says that each state is conditionally independent of previous states.

If you think about music for a minute, the Markov assumption doesn't really make sense in this context. When Bach composed his music, he probably didn't just think about the previous note. He was probably thinking about full measures, phrases and songs. To compensate, we move the Markov assumption back one and condition on the previous two states. While it's still not perfect, it strikes a balance between memory efficiency and longer-term structure. This process is also how n-gram language models work. (I wrote about n-gram models in a previous blog post)

The Model

So we've outlined how we could create a probabilistic state machine (or finite Markov process) that models Bach's chorales. The next step is to put the plan into practice. First, I took all the Bach chorales from the dataset and transpose (shift) the pitches so they would fit on the UI. Then, I created the state machine and learned the proabilties as described above. Now we have a finite state machine that uses a relaxed Markov assumption to calculate conditional probabilities for all state changes. The model is ready to generate music. To help visualize this, I've made a simplified diagram of the probabilistic state machine underlying the music model.

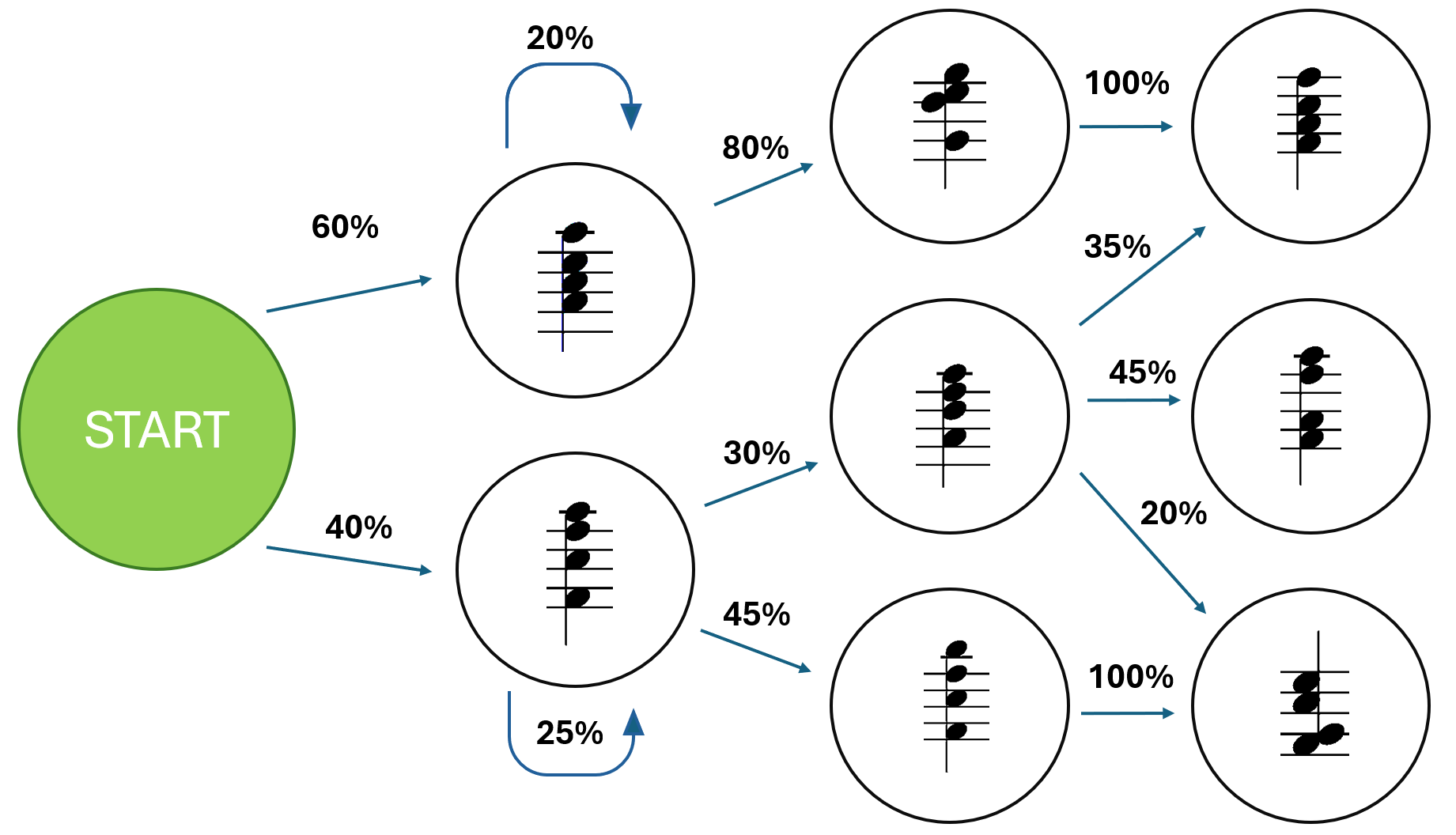
Actually generating music from the model is a relatively simple process. We start in the initial state of the graph, which is a special node that represents "before the beginning of a song". From there we see a bunch of state changes, each with their relative probabilites. We sample the next state from the possible state changes. Now, we have the first chord of the song. From there, we sample a state from all of the possible changes leaving the current state (chord). That becomes the second chord in our song. We repeat the process until we've generated enough notes to fill up the user interface.

Because the chorales dataset is modeled beat-by-beat, the generated music plays each note at each timestep. This doesn't match how Bach wrote his chorales. To compensate for this, we take one last step after generation and smooth all of the notes together. If there are two or more consecutive beats that play the same note, those notes are combined into one longer note. This leaves us with richly textured polyphonic music that sounds much more like Bach.

Results

I decided to name my little program BachByte. Try it here. You can use it on a computer or a phone, but it will work better on a computer. All you have to do is hit the generate button and the state machine will automatically generate you an original Bach-sounding chorale. Hit the play button to listen to it. You can change between six playback instruments: synthesizer, piano, pipe organ, orchestra, brass, and guitar. You can also change the tempo using the little slider.

I think the music sounds substantively like Bach. It has a few issues that all have to do with the Markov assumption. Since we only remember the last two beats, the model lacks long-term structure. It doesn't write songs with repeating motifs or an A-B-A pattern. Similarly, it will sometimes hold chords for a really long time since it can't 'remember' holding the chord for more than two beats. That being said, the music sounds pretty good. It demonstrates the power you can get using very simple modeling techniques.

In case you haven't tried BachByte yet, do it!

Note: BachByte doesn't seem to work on Safari. Please try another browser such as Chrome or Firefox.