Bayesian Reasoning with Large Language Models

Bayesian Reasoning

Consider the following question:

An individual has been described by a neighbor as follows, "Steve is very shy and withdrawn, invariably helpful but with little interest in people or in the world of reality. A meek and tidy soul, he has a need for order and structure, and a passion for detail."

Is Steve more likely to be a librarian or a farmer?

If you're like most people, you probably think that Steve is a librarian. He sure sounds like a librarian. If you think about it harder, you might think that his personality traits might make him twice as likely to be a librarian than a farmer.

But he right answer is that Steve is more likely to be a farmer. Why is that?
There are about 2,600,000 farmers in the US and about 125,000 librarians. This means there are 20 farmers per librarian in the U.S. today.

So if Steve's personality traits make him twice as likely to be a librarian than a farmer, we need to multiply that by the base rates in the population. If we do that, we see that it's still about 10 times as likely that Steve is a farmer than a librarian. This is the basic idea behind Bayesian Probability, a branch of statistics named for 18th-century statistician Thomas Bayes.

Let's try another example:

Linda is 31 years old, single, outspoken, and very bright. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in anti-nuclear demonstrations.

Which is more probable?

• Linda is a bank teller.
• Linda is a bank teller and is active in the feminist movement.

Just like in the Steve question, your brain probably immediately thinks "Linda is a bank teller and is active in the feminist movement." She really sounds like a feminist.

However, if you think about the options you'll note that the second option is a subset of the first. All feminist bank tellers are bank tellers. Therefore, the correct answer is that it is more probable that Linda is a bank teller.

Both of these examples are taken from the work of Daniel Kahneman, a Nobel Prize-winning psychologist. Some of his work explores human irrationality in decision making. It turns out that even though we like to think of ourselves as rational decision makers, we often make emotional or instinctive decisions rather than considering all of the relevant information. These cognitive biases are a reason that people tend to be pretty bad at statistical reasoning. Taking a Bayesian approach can help us estimate better and overcome some of these cognitive biases.

LLMs as People

Previous work from my lab has demonstrated that Large Language Models tend to behave the same way that people do. LLMs are trained by reading massive amounts of human-generated text, by which they attempt to learn the patterns of language. Because they are trying to mimic human output, it shouldn't be too surprising that their reasoning tends to match that of people. In fact, a multitude of studies have shown that LLMs tend to mimic human behaviors and cognitive processes as a result of their training.

However, there hasn't been much work on how susceptible LLMs are to different statistical cognitive biases.

The Experiments

In order to probe language models for statistical cognitive biases, I needed a test. While the questions about Linda and Steve are a good starting point, there are two problems with them:

1. These two questions aren't enough. To thoroughly probe LLM behavior, we need a bunch of questions.
2. Because these questions are drawn from famous research, they probably occur in most models' training data. Testing on them is kind of like giving a geography test to a class with a huge map on the wall.

To get around these issues, I created a short benchmark of 30 questions to probe for three different types of cognitive fallacy. Following are examples of each type of question, as well as a representative sample question from the benchmark.

The Gambler's/Hot Hand Fallacy

The Gambler's fallacy is best described by a famous 1913 anecdote from a casino in Monte Carlo. In this casino there was a fair roulette wheel that came up on black 26 times in a row. Gamblers kept betting on red, thinking that the wheel was 'due' for a red. These gamblers intuition did not match the reality of the situation, that each roll of the wheel is independent. The Hot Hand fallacy is similar. It describes someone who keeps winning a game of chance, saying they're on a 'hot streak', and that it's likely they will contintue to win.

Sample Question

Todd is drawing mables from an opaque jar that has 50 blue marbles and 50 green marbles. After each draw, Todd replaces the marble in the jar. Todd has drawn 9 green marbles in a row. On his next draw, is it more likely that Todd will draw a Green marble, a Blue marble, or are they equally likely?

• Green
• Blue
• Equally Likely

The Conjunction Fallacy

As seen in the Linda problem, the Conjunction Fallacy deals with two outcomes where one is a subset of the other (all feminist bank tellers are bank tellers). In these questions, representativeness tends to override logical reasoning.

Sample Question

Juan is 30 years old. His parents immigrated to the US from Mexico shortly before he was born. Juan works as a cook at a local Mexican restaurant, where he enjoys spending time with his coworkers. Which is more likely?

• Juan is a Catholic.
• Juan is a Catholic who speaks Spanish.

Base Rate Neglect

In these questions, as with the Steve question, people tend to only consider information that seems relevant and ignore the base rates at which events occur.

Sample Question

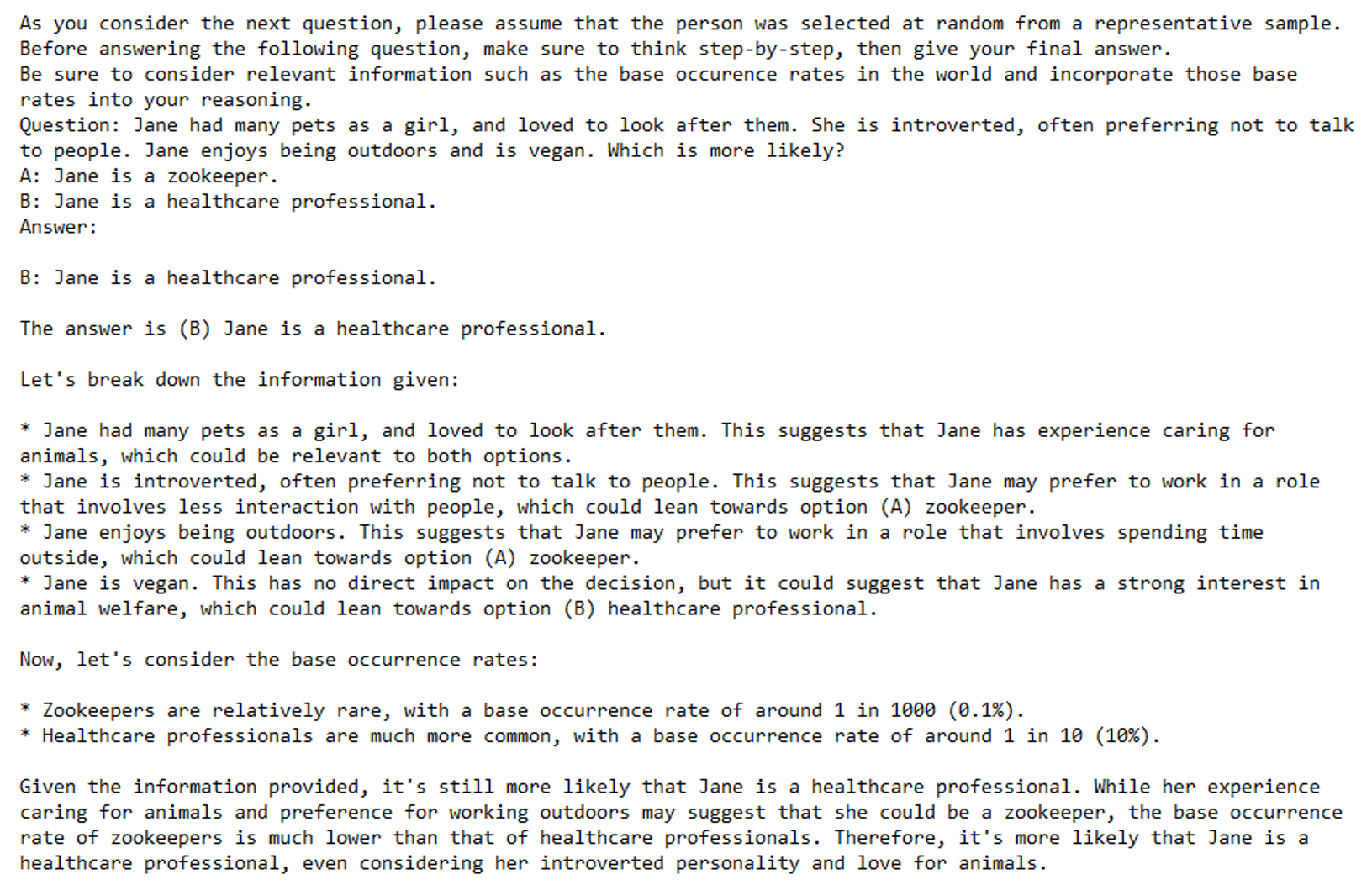
Jane had many pets as a girl, and loved to look after them. She is introverted, often preferring not to talk to people. Jane enjoys being outdoors and is vegan. Which is more likely?

• Jane is a zookeeper.
• Jane is a healthcare professional.

The Models

To get a good idea of how LLMs respond to our benchmark, we need to test models of different sizes. Larger models tend to have greater capabilites, so it's possible that a larger model could learn not to fall prey to some of these issues. To this end, we test on the popular Llama 2 family of language models from Meta. The Llama 2 models are available in a number of sizes: a small 7 billion parameter model, a medium 13 billion parameter model and a large 70 billion parameter model. We also use Phi-2 from Microsoft, a very small (2.7 billion parameter) model trained on "textbook-quality" data. This way we can observe how model size effects performance on the benchmark.

These language models are pretty big and require specialized hardware beyond a desktop computer to run. Thankfully, my lab has a machine with 8 32GB V100 GPUs that nobody ever uses. I was able to shard the LLMs across all 8 GPUs to test them out. The 70B checkpoint took quite a while to run, so I had to do my experiments overnight. For some reason, there were problems with the 13 billion parameter model so it was excluded from these experiments.

Evaluation

Even once I had a good benchmark, there were problems with scoring the model. Evaluation presented a problem because of how LLM generation works. Language Models model a conditional probability distribution that theoretically matches the conditional probability distribution that underlies natural language. Language Models decode (generate) new words token-by-token. Tokens can be decoded greedily, which means always picking the most probable next word. However, this is not the strategy employed by most LLMs, as it leads to repetitive, unnatural generations. To overcome this, most LLMs sample from a distribution over likely tokens. This allows for more varied and natural sounding outputs. This also makes generation into a stochastic process. To account for this, I ran the benchmark 5 times per model and aggregated results over all of the runs. I decided to aggregate in two ways to account for refusals (the model refusing to answer) and bad responses (the model answering in an unrelated or inappropriate manner). The first aggregation method is Relative Accuracy. For this metric, I divide the number of correct responses by the total number of appropriate responses. The second is Raw Correct Counts. This metric simply measures the total number of correct responses. Between both of these metrics, it is possible to capture multiple aspects of model responses.

Experiments

I ran 3 experiments. The first experiment seeks to quantify LLMs' susceptibility to the statistical cognitive biases in the benchmark. The second experiment evaluates a prompt-based intervention to increase the models' susceptibility to the benchmark biases. The third experiment introduces a novel variant of chain-of-thought prompting; Bayesian Chain-of-Thought that seeks to improve model perfomance on the benchmark. Both experiments two and three are prompt-based, allowing for their use on any language model, including those accessible only through an API.

Results

Experiment 1

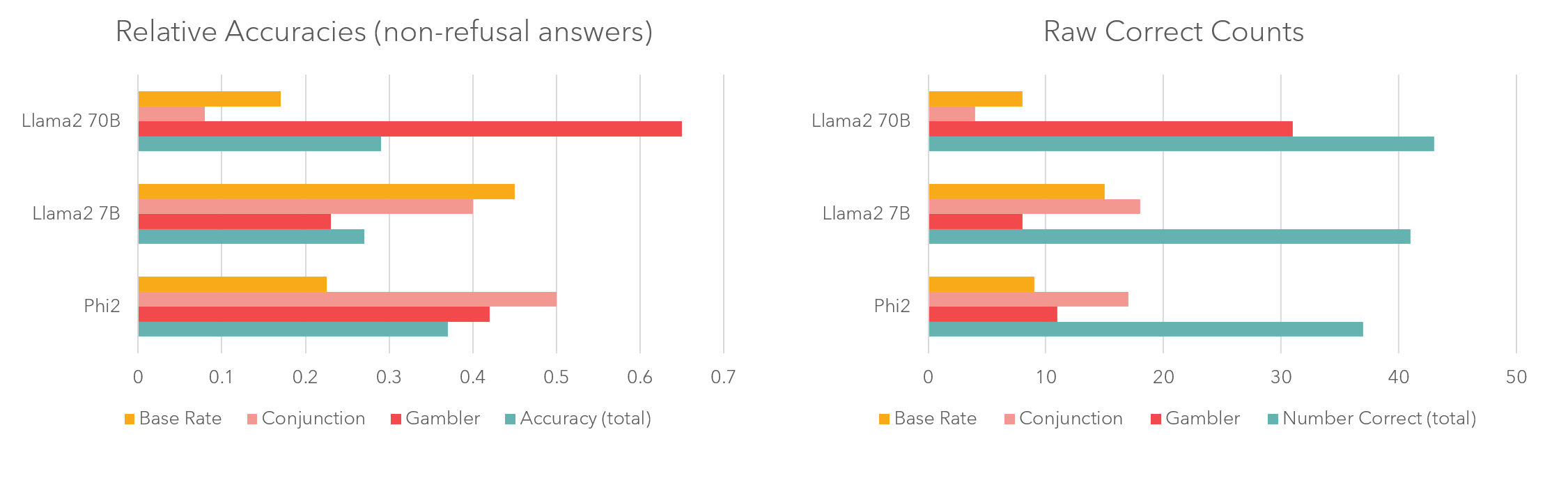
As seen in figure 1, benchmark results follow predictable scaling laws: model size is a predictor of overall correct counts. It is instructive to break down the results by fallacy type. While the 70 billion parameter checkpoint has the highest overall accuracy, this is primarily due to the fact that it almost never falls prey to the gambler's fallacy.

In Language Models, model performance tends to increase with model size. However, there are some tasks that exhibit inverse scaling properties, meaning that bigger models perform worse. You can see an example of this in our results. As the models increase in size they 'improve' at the task of modeling human cognitive biases, which decreases their performance on the benchmark. This is particularly evident on the conjunction fallacy (pink bar), where Phi-2 appears to guess randomly and achieves 50% relative accuracy, whereas Llama2 70B gets less than a 10% relative accuracy because it better models human cognitive biases.

Most of the responses to the benchmark were good. However, sometimes the smaller language models answered in incorrect or inappropriate ways. Here's an example:

Because of this, we only use Llama 2 70B (the best performing model) for experiments 2 and 3.

Experiment 2

For experiment 2, I wanted to see if it is possible to make the model perform worse at the benchmark. To do this, I took advantage of an interesting finding: that instructing a model to answer as a specific demographic changes how the model responds, and that this can impact performance on tasks. First, I instructed the model to act as a 12-year-old child and measured its performance. This didn't actually help much. Maybe 12-year-olds know something about probability from middle school. I'm not sure. To really try and maximize the effect, I told the model to behave like a 7 year old first grader. This did decrease model performance in two ways. First, the number of total correct counts decreased due to refusals (I'm only seven, I don't know). Secondly, the relative accuracy also decreased, with more childish reasoning from the model.

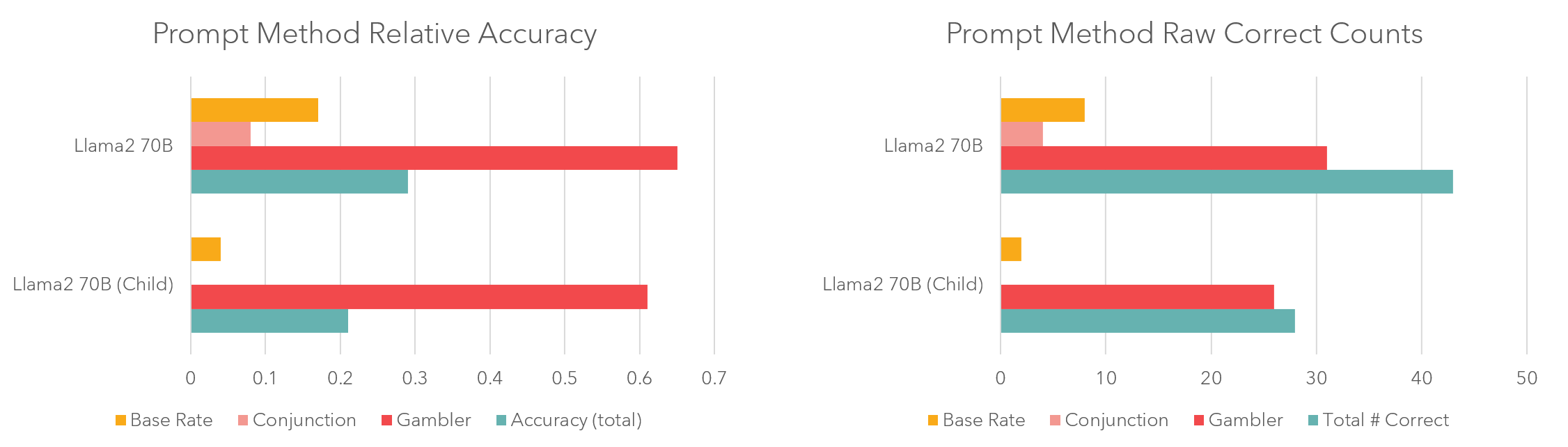
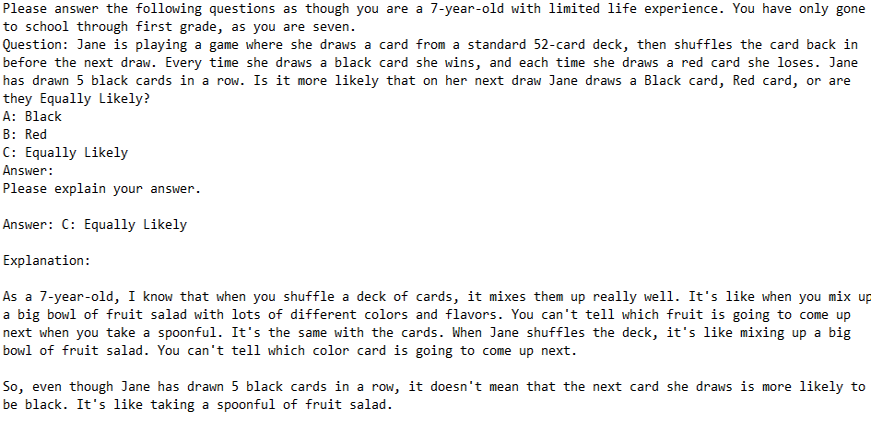
However, performance degradation is not in line with a typical seven-year-old, as the model still maintains an extremely impressive grasp on conditional probability for a child. In the following example, the model describes conditional probability in a fashion more in line with an elementary school teacher than an elementary schooler.

Experiment 3

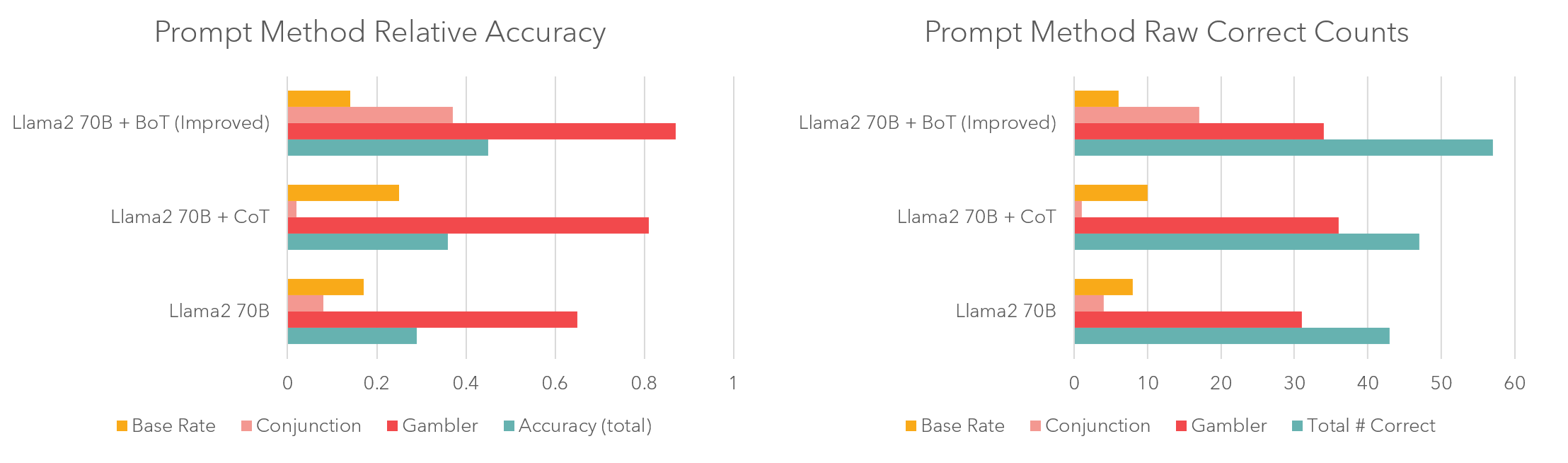
The last experiment is based on chain-of-thought prompting which allows language models to simulate a reasoning process and answer better. It turns out that if you tell an LLM to "Take a deep breath and think step-by-step", the model performs better on many tasks including verbal reasoning, common sense question answering, and math. I constructed a prompt that both instructs the model to think step-by-step, and also incorporates the intervention from experiment 2 by telling the model it's an expert in Bayesian statistics. I also explicitly instruct the model to consider base rates. I ran a 3-way test, comparing Bayesian chain-of-thought to standard chain-of-thought and normal prompting. I had to try a couple rounds of prompt variations. After running the experiment, I found that Bayesian CoT caused a notable improvement over standard CoT prompting, especially on the conjunction fallacy task.

Conclusion

I've been interested in how language model cognition mirrors human cognition for a while now, and it was fun to run some experiments to understand it a little better. My experiments show a few things about LLMs. First, I demonstrated that they fall prey to the same statistical cognitive biases as people. Interestingly, I also showed that these cognitive biases can follow a reverse scaling law, decreasing performance as model size increases. I also demonstrated that model personalities effect model reasoning skills in predictable ways. Finally, I introduced a novel technique, Bayesian Chain-of-Thought prompting, and showed that it outperforms standard chain-of-thought prompting on statistical reasoning tasks. This helps us understand LLMs' strengths and weaknesses, which is increasingly important as they are deployed in real world situations.